Ursprünge der Preispsychologie kommen aus der Spieltheorie
Kaushik Basu wandte 1997 die Spieltheorie an, um zu argumentieren, dass rationale Verbraucher ihre eigene Zeit und Mühe beim Rechnen schätzen. Solche Verbraucher verarbeiten den Preis von links nach rechts und neigen dazu, die letzten beiden Ziffern des Preises gedanklich durch eine Schätzung des mittleren “Cent-Anteils” aller Waren auf dem Markt zu ersetzen. Quelle: https://en.wikipedia.org/wiki/Psychological_pricing
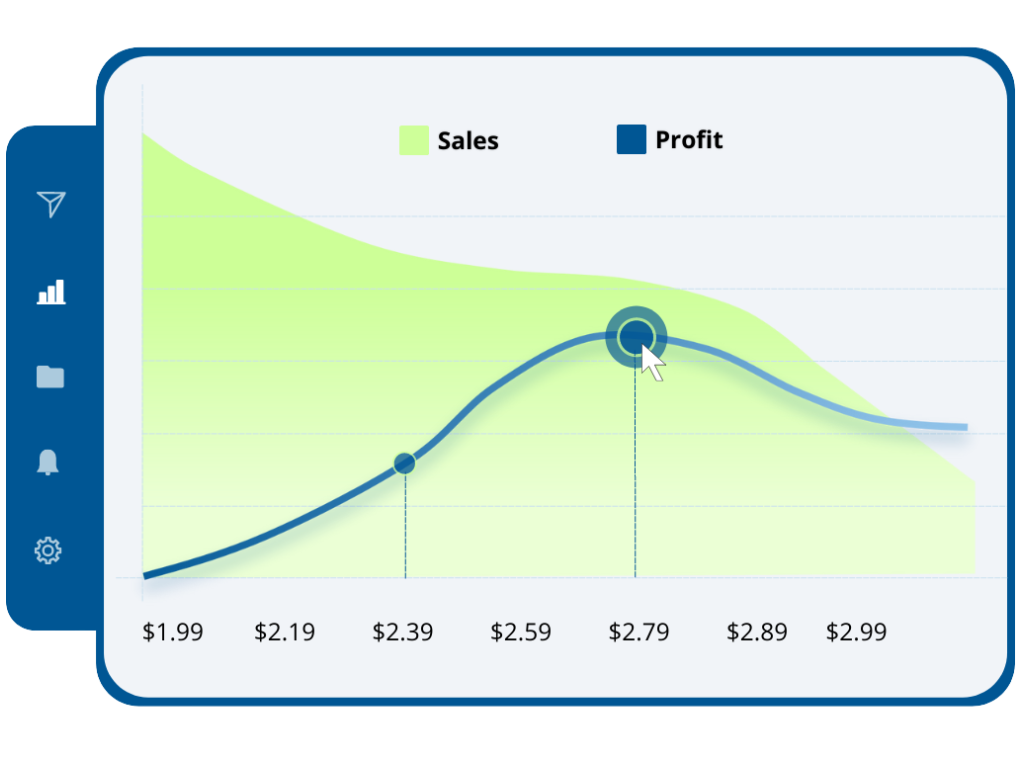
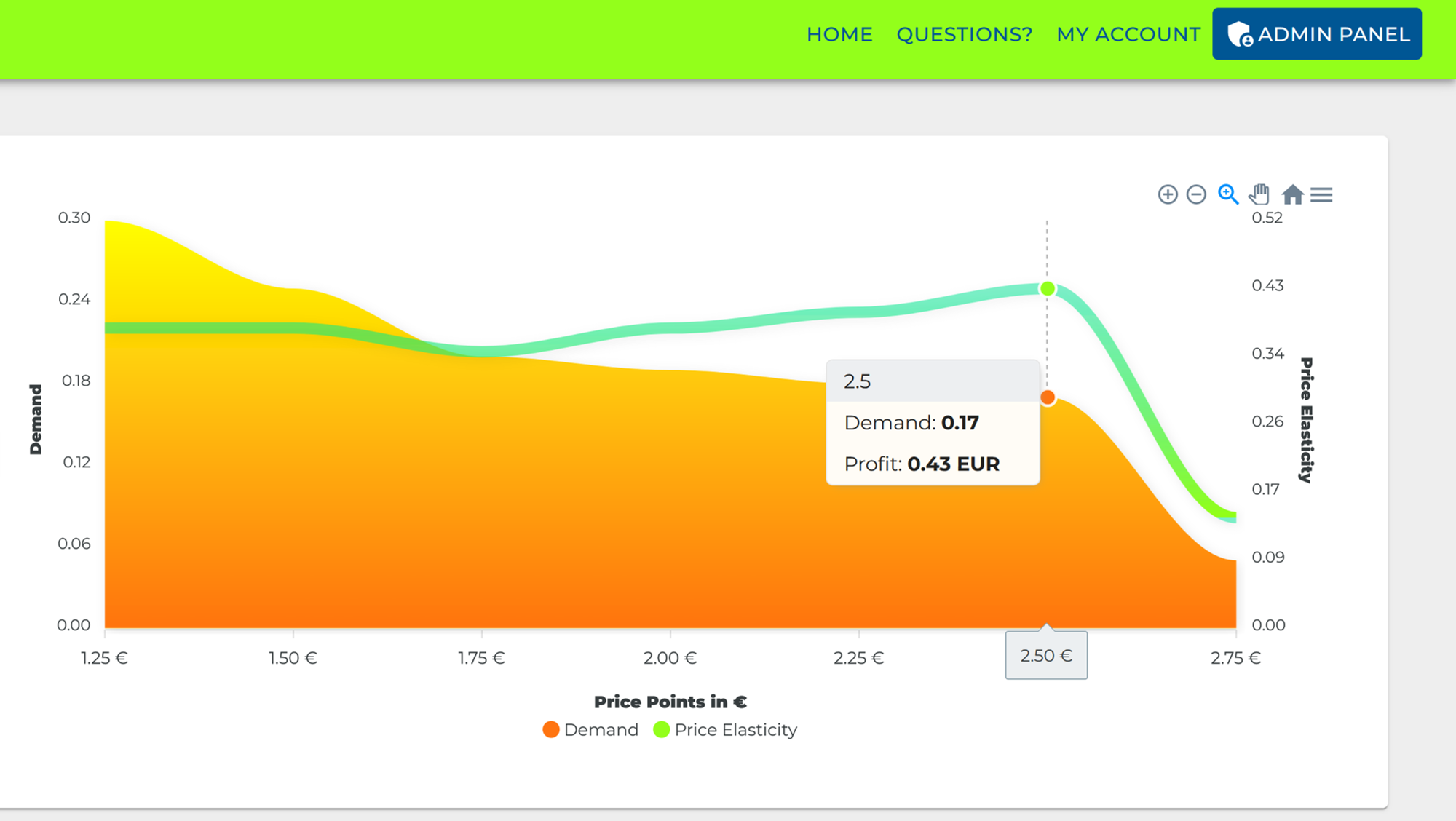
Diese psychologische Preisgestaltung senkt die Preise oft als Zahlen direkt unter “ganze” Zahlen, also Zahlen, die etwas kleiner als eine runde Zahl sind, z. B. 9,99 € oder 19,99€. Kunden neigen dazu, Preise, die niedriger als sie tatsächlichen sind, auf die nächstniedrigere Geldeinheit zu runden, obwohl der absolute Preisunterschied kaum relevant ist. Daher können Preise wie 1,99 € dazu führen, dass sie als eher als “1€”, als als “2€” wahrgenommen werden.
Diese Schätzung ist abhängig von der Erfahrung und dem Wissen des Einzelnen und in der Regel eine subjektive Wahrnehmung. Durch diese Annahme lässt sich erklären, warum Verbraucher bei einem Preis von 12,99€ weniger verhandeln werden, als bei einem Preis von 13,00€. Auch wenn diese Theorie auf den ersten Blick plausibel erscheint, so ist sie doch mit einigen Schwächen behaftet. Zum einen ist die These nur dann valide, wenn der Preis von links nach rechts gelesen wird. In vielen Kulturen jedoch wird der Preis von rechts nach links gelesen, was die gesamte Argumentation in Frage stellt.
Der Labortest von Ruffle und Shtudiner (2006) zeigt, dass Basus Gleichgewicht der 99-Cent-Preise erheblich unterstützt wird.
Benfordsches Gesetz
Das Benfordsche Gesetz besagt, dass in vielen realen numerischen Datensätzen die führende Ziffer wahrscheinlich klein ist. In Datensätzen, die dem Gesetz gehorchen, erscheint die Zahl 1 in etwa 30 % der Fälle als führende signifikante Ziffer, während die Zahl 9 in weniger als 5 % der Fälle als führende signifikante Ziffer erscheint. Wären die Ziffern gleichmäßig verteilt, würden sie jeweils etwa 11,1 % der Zeit vorkommen. Das Benfordsche Gesetz macht auch Vorhersagen über die Verteilung von zweiten Ziffern, dritten Ziffern, Ziffernkombinationen usw.
Dieses Ergebnis gilt für eine breite Palette von Datensätzen – von Stromrechnungen bis hin zu Sterberaten. Dies wurde durch eine Vielzahl von Studien bewiesen, die unterschiedliche Faktoren untersucht haben. Durch die Betrachtung verschiedener Konstanten konnten die Forscher ermitteln, dass dieses Ergebnis in den meisten Fällen zutrifft.
Das Gesetz ist nach Frank Benford, einem Physiker, benannt, der es 1938 in einer Abhandlung mit dem Titel “The Law of Anomalous Numbers” (Das Gesetz der anomalen Zahlen) formuliierte. Allerdings war es bereits 1881 von Simon Newcomb formuliert worden.
Das Gesetz ist vom Konzept her dem Zipf’schen Gesetz ähnlich, wenn auch in der Verteilung nicht identisch.